- Press Ahead [C1]:
- Designated dancers move one position forward.
- Press Back [C1V]:
- Designated dancers move one position backward.
Press Back is typically only used as a gimmick.
- Press In|Out|Right|Left [C2]:
- As one movement, designated dancers move one position forward and one position
toward the given direction.
Notes:
-
Non-designated dancers do not move or adjust in any manner.
-
Do not change your facing direction during this call.
-
'Position' in terms of this definition refers to a spot that could be
occupied by a dancer. Within a 2 x 4 there are eight positions. A
Squared Set, Butterfly, or "O" is a 16-Matrix (4 x 4)
formation, and one position refers to an adjacent spot within that
rectangular grid.
-
The direction can be In, Out, Right, or Left. In and
Out are relative to the Center of the Set.
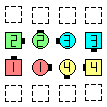
| |
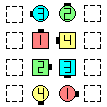
| before
Press Right | | after
|
|
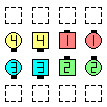
| |
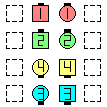
| before
Press Left | | after
|
|
The following examples illustrate the differences among the similar calls
Extend, 1/2 Press Ahead, and Step Thru.

| This is the starting formation
for each of the following: | | |
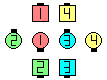
| |
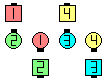
| |

| after
Extend | | after
1/2 Press Ahead | | after
Step Thru |
|
Often callers misuse the term Extend when they mean to use
Press Ahead or 1/2 Press Ahead.

| This is the starting formation
for each of the following: | | |
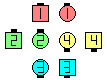
| |
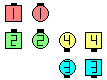
| after
As Couples Extend | | after
1/2 Press Ahead |
|
Curve direction [C4] (Dave Hodson 1985):
As one movement, Press direction while individually turning toward that direction.
Direction can be In, Out, Left, or Right and is relative to the Center of the Set.
Tip Toe [C4] (Lee Kopman 1980):
Designated dancers Press Ahead while holding onto the dancer in their
partner's position, dragging that dancer with them.
See also direction Loop n [C2]
and Truck [C2].